4753. Cinema+

Once the pupils of the B-th school of city G decided to go to cinema. Cinema Administration has placed them in the hall of size n × m, which has been specially selected so that all the seats were occupied by pupils. Each cinema visitor was given a number.

Pupils took their places in the following way: they entered the hall in the order of their numbers, and fully occupied initially the first row, then second row, then third row, etc.

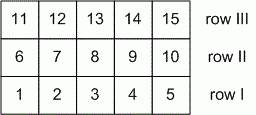
However the class teacher decided that such seating is bad for the behavior of pupils and replaced them in another way: the pupils first occupied all the first places of each row, then all the second places in each row, etc. (see picture).

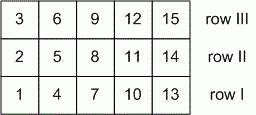
The administration has decided to find out how many pupils do not change their place after replacement.

Input. First line contains numbers n and m (1 ≤ n, m ≤ 10⁹).

Output. Print the number of pupils whose seat was not changed after replacement. Print the number of pupils whose seat was not changed after replacement.

Sample input 1	Sample output 1
3 4	2
Sample input 2	Sample output 2
3 3	3

SOLUTION

mathematics - GCD

Algorithm analysis

Let’s fill two two-dimensional arrays as stated in the problem statement (0 ≤ i < n, 0 ≤ j < m):

· fill array c1 how the schoolchildren sat down: c1[i][j] = i * m + j + 1;

· fill array c2 how the class teacher replaces the children: c2[i][j] = j * n + i + 1;

Equate c1[i][j] and c2[i][j]:

i * m + j + 1 = j * n + i + 1,

i * (m – 1) = j * (n – 1), i / j = (n – 1) / (m – 1) = p / q,

where p / q – is irreducible fraction. Hence

, 0 ≤ l ≤ min((n – 1) / p, (m – 1) / q)

Let d = GCD(n – 1, m – 1), then or .

Therefore 0 ≤ l ≤ min((n – 1) / p, (m – 1) / q) = min(d, d) = d. The number of such l for which exists the pair (i, j) = (pl, ql) such that c1[i][j] = c2[i][j], equals to d + 1.

Example

Let the cinema sizes are n = 19, m = 7.

Then d = GCD(n – 1, m – 1) = GCD(18, 6) = 6. The fraction p / q equals to 18 / 6 = 3 / 1 (p = 3, q = 1). The pairs (i, j) such that c1[i][j] = c2[i][j] or i * m + j + 1 = j * n + i + 1, will be (pl, ql) = (3l, l), where 0 ≤ l ≤ 6:

l = 0: (i, j) = (0, 0);	l = 4: (i, j) = (12, 4);
l = 1: (i, j) = (3, 1);	l = 5: (i, j) = (15, 5);
l = 2: (i, j) = (6, 2);	l = 6: (i, j) = (18, 6);
l = 3: (i, j) = (9, 3);

Algorithm realization

Read the input data.

scanf("%lld %lld",&n,&m);

Find and print the answer, that equals to GCD(n – 1, m – 1) + 1.

d = gcd(n-1,m-1);

printf("%lld\n",d+1);